| |

Integral Calculus
Integral calculus is that portion of "the" calculus dealing with
integrals
Among his many other talents, Major General Stanley in Gilbert and Sullivan's operetta The Pirates of Penzance impresses the pirates with his knowledge of calculus in "The Major General's Song" as follows: "I'm very good at integral and differential calculus, I know the scientific names of beings animalculous; In short, in matters vegetable, animal, and mineral, I am the very model of a modern Major-General."
Integration is an important concept in mathematics and, together with differentiation, is one of the two main operations in calculus. Given a function ƒ of a real variable x and an interval [a, b] of the real line, the definite integral

is defined informally to be the net signed area of the region in the xy-plane bounded by the graph of ƒ, the x-axis, and the vertical lines x = a and x = b.
The term integral may also refer to the notion of antiderivative, a function F whose derivative is the given function ƒ. In this case, it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals.
The principles of integration were formulated independently by Isaac Newton and Gottfried Leibniz in the late 17th century. Through the fundamental theorem of calculus, which they independently developed, integration is connected with differentiation: if ƒ is a continuous real-valued function defined on a closed interval [a, b], then, once an antiderivative F of ƒ is known, the definite integral of ƒ over that interval is given by

Integrals and derivatives became the basic tools of calculus, with numerous applications in science and engineering. A rigorous mathematical definition of the integral was given by Bernhard Riemann. It is based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs. Beginning in the nineteenth century, more sophisticated notions of integrals began to appear, where the type of the function as well as the domain over which the integration is performed has been generalised. A line integral is defined for functions of two or three variables, and the interval of integration [a, b] is replaced by a certain curve connecting two points on the plane or in the space. In a surface integral, the curve is replaced by a piece of a surface in the three-dimensional space. Integrals of differential forms play a fundamental role in modern differential geometry. These generalizations of integral first arose from the needs of physics, and they play an important role in the formulation of many physical laws, notably those of electrodynamics. There are many modern concepts of integration, among these, the most common is based on the abstract mathematical theory known as Lebesgue integration, developed by Henri Lebesgue.
TABLE OF INTEGRALS
Power of x.
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) xn dx = xn+1 (n+1)-1 + C xn dx = xn+1 (n+1)-1 + C
(n 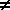 -1) Proof -1) Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) x-1 dx = ln|x| + C x-1 dx = ln|x| + C |
Exponential / Logarithmic
Trigonometric
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sin x dx = -cos x + C sin x dx = -cos x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) csc x dx = - ln|csc x + cot x| + C csc x dx = - ln|csc x + cot x| + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) cos x dx = sin x + C cos x dx = sin x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sec x dx = ln|sec x + tan x| + C sec x dx = ln|sec x + tan x| + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) tan x dx = -ln|cos x| + C tan x dx = -ln|cos x| + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) cot x dx = ln|sin x| + C cot x dx = ln|sin x| + C
Proof |
Trigonometric Result
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) cos x dx = sin x + C cos x dx = sin x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) csc x cot x dx = - csc x + C csc x cot x dx = - csc x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sin x dx = -cos x + C sin x dx = -cos x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sec x tan x dx = sec x + C sec x tan x dx = sec x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sec2 x dx = tan x + C sec2 x dx = tan x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) csc2 x dx = - cot x + C csc2 x dx = - cot x + C
Proof |
Inverse Trigonometric
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) arcsin x dx = x arcsin x + arcsin x dx = x arcsin x + ![[sqrt] [sqrt]](http://math2.org/math//symbols/sqrt.gif) (1-x2) + C (1-x2) + C |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) arccsc x dx = x arccos x - arccsc x dx = x arccos x - ![[sqrt] [sqrt]](http://math2.org/math//symbols/sqrt.gif) (1-x2) + C (1-x2) + C |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) arctan x dx = x arctan x - (1/2) ln(1+x2) + C arctan x dx = x arctan x - (1/2) ln(1+x2) + C |
Inverse Trigonometric Result
Hyperbolic
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sinh x dx = cosh x + C sinh x dx = cosh x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) csch x dx = ln |tanh(x/2)| + C csch x dx = ln |tanh(x/2)| + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) cosh x dx = sinh x + C cosh x dx = sinh x + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) sech x dx = arctan (sinh x) + C sech x dx = arctan (sinh x) + C |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) tanh x dx = ln (cosh x) + C tanh x dx = ln (cosh x) + C
Proof |
![[integral] [integral]](http://math2.org/math//symbols/integral.gif) coth x dx = ln |sinh x| + C coth x dx = ln |sinh x| + C
Proof |
OTHERS:
TUTORIALS:
|
|
 |
|
is an engineering discipline which uses the scientific knowledge of the behavior and effects of electrons to develop components, devices, systems, or equipment (as in electron tubes, transistors, integrated circuits, and printed circuit boards) that uses electricity as part of its driving force. Both terms denote a broad engineering field that encompasses many sub fields including those that deal with power, instrumentation engineering, telecommunications, semiconductor circuit design, and many others.
- http://en.wikipedia.org/wiki/Electronic_engineering |
|
|
 |
 |
|

